CIFRADO ASIMÉTRICO

INTRODUCCIÓN

En esta investigación nos iremos a fondo con una de las técnicas más utilizadas para poder proteger la integridad y la privacidad de nuestros datos, nos referimos a los cifrados asimétricos, en donde podremos ver diferentes tipos, tales como el cifrado RSA, el Diffie-Hellman key exchange, entre otros. 

Antes de ver los diferentes cifrados asimétricos, recordemos qué era un cifrado asimétrico.
CIFRADO ASIMÉTRICO

La criptografía asimétrica, también conocida como criptografía de clave pública, usa claves públicas y privadas para cifrar y descifrar datos. Las claves son simplemente números grandes que se han emparejado pero que no son idénticos (asimétricos). Una clave del par se puede compartir con todos; se llama clave pública. La otra clave del par se mantiene en secreto; se llama clave privada. Cualquiera de las claves se puede usar para encriptar un mensaje; la tecla opuesta a la utilizada para encriptar el mensaje se utiliza para el descifrado. (TechTarget, 2017)

Con el paso del tiempo se han inventado varias formas de implementar el cifrado asimétrico, en donde podemos encontrar:

RSA

A diferencia de la criptografía simétrica, donde la clave es típicamente solo una serie aleatoria de bytes, las claves RSA tienen una estructura interna compleja con propiedades matemáticas específicas.

RSA (Rivest-Shamir-Adleman), es el algoritmo asimétrico más utilizado, está integrado en el protocolo SSL / TLS que se utiliza para proporcionar seguridad de comunicaciones a través de una red informática. RSA deriva su seguridad de la dificultad computacional de factorizar enteros grandes que son el producto de dos números primos grandes. Multiplicar dos números primos grandes es fácil, pero la dificultad de determinar los números originales del factorizado total forma la base de la seguridad de la criptografía de clave pública. El tiempo que lleva factorizar el producto de dos primos suficientemente grandes se considera que está más allá de las capacidades de la mayoría de los atacantes, excluyendo a los actores del estado nación que pueden tener acceso a suficiente poder de cómputo. Las claves RSA suelen tener una longitud de 1024 o 2048 bits, pero los expertos creen que las claves de 1024 bits podrían romperse en un futuro próximo, por lo que el gobierno y la industria se están moviendo a una longitud de clave mínima de 2048 bits y máxima de 4096 bits. (Blanda, 2017)

Las claves para el algoritmo RSA se generan de la siguiente manera: 

1. Elija dos números primos distintos p y q. Para que el sistema sea seguro, los enteros p y q deben elegirse al azar y deben tener una longitud de bits similar. Para encontrar números primos grandes, los números se pueden elegir al azar y, utilizando uno de varios métodos probabilísticos rápidos, podemos probar su primalidad.
2. Calcule n = pq. El producto n se usará como módulo para las claves pública y privada. Su longitud, generalmente expresada en bits, es la longitud de la clave.
3. Calcule ϕ(n) = ϕ(p) ϕ(q) = (p-1) (q-1), donde ϕ es la función indicatriz de Euler.
4. Elija un entero e tal que 1 <e < ϕ(n) y gcd (e, ϕ(n)) = 1 (es decir, e y ϕ(n) son co-primos). El número e se libera como el exponente de la clave pública.
5. Determine d como d≡e ^ {- 1} (mod ϕ(n)). Es decir, d es la inversa multiplicativa de e (módulo ϕ(n). Esto a menudo se calcula utilizando el algoritmo euclidiano extendido. El número d se mantiene como el exponente de la clave privada.

La clave pública está formada por el par (n, e), donde n se denomina módulo y e se denomina exponente público (o cifrado). La clave privada está formada por el par (n, d), donde d se denomina exponente privado (o desencriptado). Es imperativo que el exponente de descifrado d se mantenga en secreto. Además, los números p, q y ϕ(n) también deben mantenerse en privado porque se pueden usar para calcular d.Para cifrarlo primero se tiene que convertir el mensaje M en un número entero m, tal que 0≤m<n. Esto se hace mediante el uso de un protocolo reversible previamente acordado conocido como un esquema de relleno. ya calculadas sus llaves para obtener el texto cifrado se calcula cifrado≡ m^{e} (mod n). Finalmente, para descifrarlo se calcula m≡ cifrado^{d} (mod n). (TechTarget, 2017)

DIFFIE-HELLMAN KEY EXCHANGE

El intercambio de claves Diffie-Hellman (D-H) es un método seguro para intercambiar claves criptográficas. 

Este método permite que dos partes que no tienen conocimiento previo entre sí establezcan una clave secreta compartida, incluso sobre un canal inseguro.

El concepto usa un grupo multiplicativo de enteros modulo, que, sin conocimiento de las claves privadas de ninguna de las partes, presentaría una tarea matemáticamente abrumadora a un descifrador de código.

Para implementar Diffie-Hellman, se necesitan dos usuarios, mientras se comunican a través de un canal que saben que es privado, acuerdan mutuamente números enteros positivos p y q, tal que p es un número primo y q es un generador de p. El generador q es un número que, cuando se eleva a potencias positivas de números enteros menores que p, nunca produce el mismo resultado para dos de esos números enteros. El valor de p puede ser grande, pero el valor de q suele ser pequeño.

Luego cada uno de los usuarios selecciona un número entero positivo, convirtiéndose en sus llaves privadas (a y b).
Después cada usuario calcula:

• q^{a} (mod p) ≡a*
• q^{b} (mod p) ≡b*

Todo para obtener las llaves públicas que se enviaran uno al otro (a* y b*)
Finalmente, cada usuario toma la llave publica del otro y calcula:

• (b*) ^{a} (mod p) ≡x
• (b*) ^{a} (mod p) ≡x

El valor de x resulta ser el mismo según cualquiera de las dos fórmulas anteriores. Sin embargo, las claves personales a y b, que son críticas en el cálculo de x, no se han transmitido a través de un medio público. Debido a que es un número grande y aparentemente aleatorio, un hacker potencial no tiene casi ninguna posibilidad de adivinar correctamente x, incluso con la ayuda de una poderosa computadora para realizar millones de pruebas. Por lo tanto, los dos usuarios pueden, en teoría, comunicarse en privado a través de un medio público con un método de encriptación de su elección utilizando la clave de descifrado x. (Cruise, 2017)

La limitación más seria de Diffie-Hellman en su forma básica o "pura" es la falta de autenticación. Idealmente, Diffie-Hellman debe usarse junto con un método de autenticación reconocido, como las firmas digitales, para verificar las identidades de los usuarios a través del medio de comunicación público. Diffie-Hellman es muy adecuado para su uso en la comunicación de datos.

DSS

El Estándar de firma digital (DSS) es el algoritmo de firma digital (DSA) desarrollado por la Agencia de Seguridad Nacional de los EE. UU. (NSA) para generar una firma digital para la autenticación de documentos electrónicos.

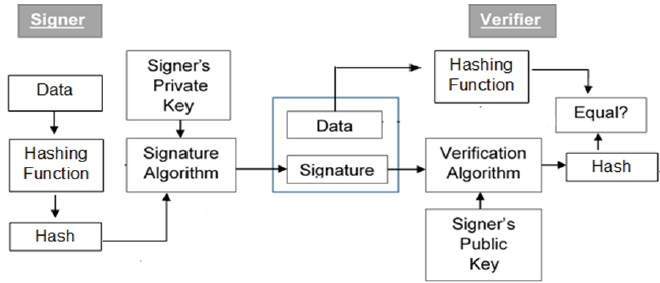
DSA es un par de números grandes que se calculan de acuerdo con el algoritmo especificado dentro de los parámetros que permiten la autenticación del signatario y, como consecuencia, la integridad de los datos adjuntos. Las firmas digitales se generan a través de DSA, así como también se verifican. Las firmas se generan junto con el uso de una clave privada; la verificación tiene lugar en referencia a una clave pública correspondiente. Cada firmante tiene sus propias claves públicas emparejadas (supuestamente conocidas por el público en general) y privadas (conocidas solo por el usuario). Debido a que una firma solo puede ser generada por una persona autorizada que usa su clave privada, la clave pública correspondiente puede ser utilizada por cualquier persona para verificar la firma. (Techopedia Inc., 2017)

DSA no encripta los resúmenes de mensajes usando claves privadas ni descifra los resúmenes de mensajes usando claves públicas. En su lugar, utiliza funciones matemáticas únicas para crear una firma digital que consta de dos números de 160 bits, que se originan a partir de los resúmenes de mensajes y la clave privada. Los DSA hacen uso de la clave pública para autenticar la firma, pero el proceso de autenticación es más complicado cuando se compara con RSA.

ECC

Criptografía de curva elíptica (ECC) es una criptografía de clave pública. En la criptografía de clave pública, cada usuario o dispositivo que toma parte en la comunicación generalmente tiene un par de claves, una clave pública y una clave privada, y un conjunto de operaciones asociadas con las claves para realizar las operaciones criptográficas.

Las operaciones matemáticas de ECC se definen sobre la curva elíptica y^2 = x^3 + ax + b, donde 4a^3 + 27b^2 ≠ 0. Cada valor de a y b da una curva elíptica diferente. Todos los puntos (x, y) que satisfacen la ecuación anterior más un punto en el infinito se encuentran en la curva elíptica. La clave pública es un punto en la curva y la clave privada es un número aleatorio. La clave pública se obtiene al multiplicar la clave privada con el punto generador G en la curva. El punto generador G, los parámetros de curva a y b, junto con algunas constantes más constituyen el parámetro de dominio de ECC. (Blanda, 2017)

Una ventaja principal de ECC es su pequeño tamaño de clave. Una clave de 160 bits en ECC se considera segura como clave de 1024 bits en RSA.

La seguridad de ECC depende de la dificultad del Logaritmo Discreto de Curva Elíptica

Por ejemplo, sean P y Q dos puntos en una curva elíptica tal que kP = Q, donde k es un escalar. Dado P y Q, es computacionalmente inviable obtener k, si k es suficientemente grande. k es el logaritmo discreto de Q a la base P.

Por lo tanto, la principal operación involucrada en ECC es la multiplicación de puntos. Es decir, la multiplicación de un escalar k con cualquier punto P en la curva para obtener otro punto Q en la curva.

La multiplicación de puntos se logra mediante dos operaciones básicas de curva elíptica

Punto de suma, sumando dos puntos J y K para obtener otro punto L, es decir, L = J + K.

Duplicar puntos, sumar un punto J a sí mismo para obtener otro punto L, es decir, L = 2J.

Punto de Suma

Duplicar Puntos

El logaritmo discreto de la curva elíptica es el problema difícil que sustenta la ECC. A pesar de casi tres décadas de investigación, los matemáticos aún no han encontrado un algoritmo para resolver este problema que mejore el enfoque ingenuo. En otras palabras, a diferencia de la factorización, basada en las matemáticas actualmente entendidas, no parece haber un atajo que reduzca la brecha en una función de puerta trampa basada en este problema. Esto significa que para números del mismo tamaño, resolver logaritmos discretos de curva elíptica es significativamente más difícil que factorizar. Dado que un problema difícil más intensivo desde el punto de vista informático significa un sistema criptográfico más fuerte, se deduce que los criptosistemas de curva elíptica son más difíciles de romper que RSA y Diffie-Hellman. (Sullivan, 2017)

CONCLUSIÓN

Podemos darnos cuenta que la mayoría de los cifrados expuestos en este ensayo se basan en problemas matemáticos de difícil resolución, por lo que podemos intuir que, entre más fuerte sea el procesamiento matemático, más seguro sería. Sin embargo, al proponer esa idea tenemos que tomar en cuenta que para ello necesitamos mejores computadoras para lograr hacer ese procesamiento, por lo que a base de esos cifrados y de los nuevos que pueden llegar, su objetivo es poder crear un cifrado ligero pero que a la vez sea difícil de resolver sin ocupar enorme procesamiento. Ahora en base a los cifrados que tenemos aquí, cada uno tiene sus ventajas y desventajas, pero para poder elegir uno depende demasiado en el sistema en el que se le va a implementar dicha seguridad y el uso que se le va dar, de este modo tendremos un sistema balanceado en base a sus necesidades y robusto.

Referencias

Blanda, S. (22 de 10 de 2017). RSA Encryption – Keeping the Internet Secure. Obtenido de AMS Blogs "American Mathematical Society": https://blogs.ams.org

Cruise, B. (22 de 10 de 2017). Diffie-hellman key exchange. Obtenido de khanacademy: https://www.khanacademy.org

Cryptography.io. (22 de 10 de 2017). Asymmetric algorithms. Obtenido de Cryptograpy: https://cryptography.io

SSL2BUY. (22 de 10 de 2017). ECC Algorithm to Enhance Security with Better Key Strength. Obtenido de SLL2BUY "Global SSL provider": https://www.ssl2buy.com

Sullivan, N. (22 de 10 de 2017). A (relatively easy to understand) primer on elliptic curve cryptography. Obtenido de Ars Technica: https://arstechnica.com

Techopedia Inc. (14 de 10 de 2017). DSA. Obtenido de Technopedia: https://www.techopedia.com

TechTarget. (22 de 10 de 2017). Asymmetric Cryptography. Obtenido de TechTarget | Search Security: http://searchsecurity.techtarget.com